Significant Findings
Principle of Reciprocity applied to the Einstein Ring Calculation
the general and special cases
Impact Parameter (Defined)
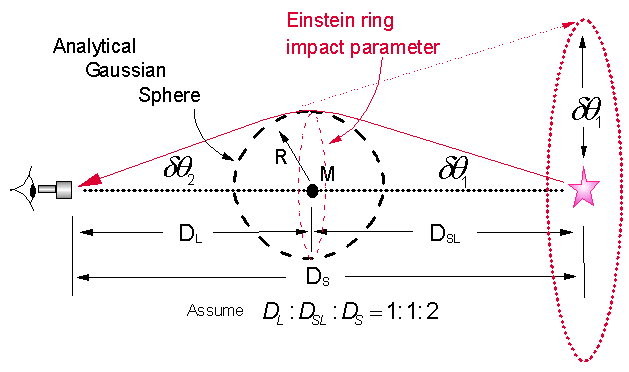
Fig 2 Symmetry Requirement of Lensing Demonstrated
From Fig 2 the total deflection of the light ray, and thus the total angle of gravitational deflection representing the accumulative effect of gravitation on the light ray is give as
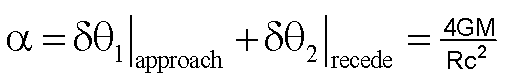
In this example the gravitating mass M is chosen to be positioned at the midpoint on the line of length DS joining the observer and the source. The astronomical distance DL is the distance from the observer to the lens and DSLis the distance from the lens to the source. Also again, it is important to note that this case is only a simplified case, by setting DL = DSL, presented in most academic textbooks. There is no requirement at all that the lens be positioned exactly at the midpoint for an observation of a theoretical Einstein ring. Of course, this again would assume the validity of the light bending rule of General Relativity. This will become much more clearer in the next section that addresses the axis of symmetry of the lensed light ray for corresponding near- and far observers. It is readily seen that the axis of symmetry for a given light ray is perpendicular to the line joining the source and the observer only for the special case where the lens is positioned at the midpoint.
In this example, the radius R of the analytical Gaussian sphere enclosing the gravitating mass M is related to the angle h under which an astronomical object of that size might appear to an observer and is given by
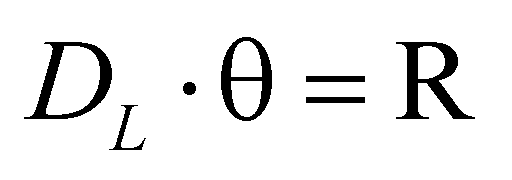
where R and DL are expressed in meters and the angle is expressed in radians.
The impact parameter for all the light rays that would be responsible for producing an image of an Einstein ring would simply be R. This is the nearest point of approach of the light rays to the center of the gravitating mass M. Since we are dealing with small angles, from Fig 2, the deflection of the light ray due to the gravitational effect on approach to the gravitating mass is just simply
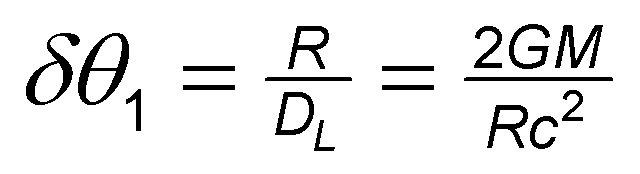
From symmetry we have
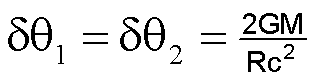
Solving for the radius of the impact parameter of the light ray and thus the radius of the Einstein Ring expressed in radians we have
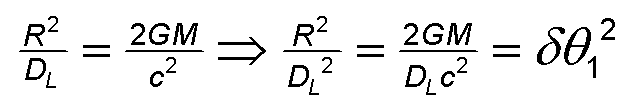
and finally
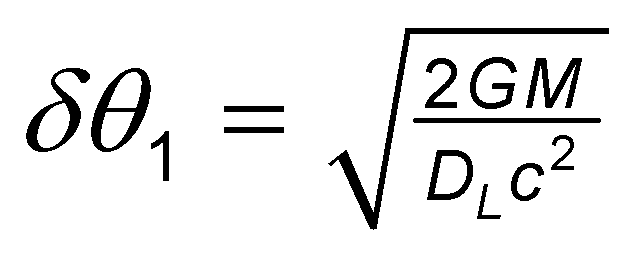
It is important to note that this is the simplified special case presented in most textbooks, where DL = DSL , where DL is the distance between the observer and the lens and DSL is the distance between the light source and the lens, placing the lens exactly halfway between the light source and the observer.
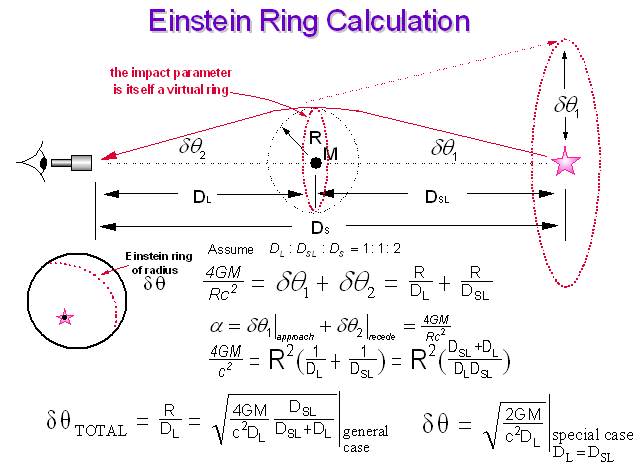
Fig 2B Einstein Ring Calculation; the General Case
Note that the angle of deflection for the approach segment, one half of the total gravitational effect, is exactly equal to the radius of the solved Einstein ring for the special case expressed in radians and is given as
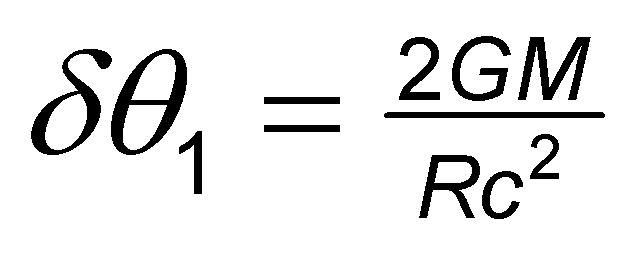
This principle, an essential Mathematical Physics principle on lensing, is often totally missed by researchers attempting to deal with this topic. From symmetry requirement, the gravitational effect on a light ray upon approach to a gravitating mass positioned exactly at the midpoint of a line joining the source and the observer, must equal that of the gravitational effect on the light ray upon receding the gravitating mass, whereby
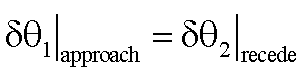
and thus,
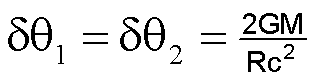
This is a rarely covered fundamental on gravitational lensing in modern academic textbooks. The accumulative effect must sum the effects on the light ray upon approach and receding the gravitating mass. From above, the total accumulative effect is thus
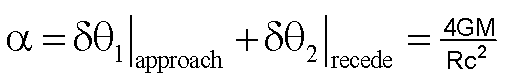
In this example, the radius R of the analytical Gaussian sphere enclosing the gravitating mass M is related to the angle h under which an astronomical object of that size might appear to an observer and is given by
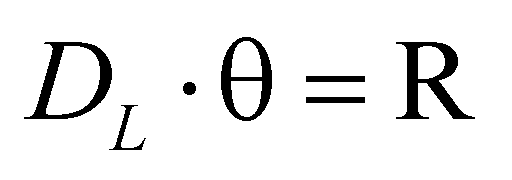
where again R and DL are expressed in meters and the angle is expressed in radians.
The impact
parameter , i.e., the nearest point of approached observed for
bent optical starlight rays to the gravitating mass, where
![]() is
the impact
parameter, again expressed in radians, for all the light rays that would be responsible for producing
an image of an Einstein ring. The impact
parameter in Figures 2 and 2B would in itself be a virtual ring of radius
R,
the same radius of the Gaussian sphere that encloses the mass M.
Note, the impact parameter here,
is
the impact
parameter, again expressed in radians, for all the light rays that would be responsible for producing
an image of an Einstein ring. The impact
parameter in Figures 2 and 2B would in itself be a virtual ring of radius
R,
the same radius of the Gaussian sphere that encloses the mass M.
Note, the impact parameter here, ![]() (in radians), is equated to the radius R (in radians) of the solar mass
M, where
(in radians), is equated to the radius R (in radians) of the solar mass
M, where
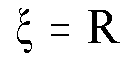 (2)
(2)
as is given by equation
(2) in the section below titled "A Flawed Tool". R is the impact
parameter and is the smallest value for ![]() and
is the nearest point of approach historically observed for light rays to the center of the
gravitating mass M.
and
is the nearest point of approach historically observed for light rays to the center of the
gravitating mass M.
Since we are dealing with astronomical distances and small angles, from Fig 2, the special case, the deflection of the light ray due to the gravitational effect on approach to the gravitating mass is just simply
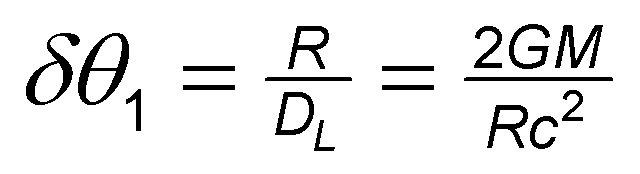
again expressed in radians. A correct understanding of this important subject that has been erroneously taught in academia and erroneously published in the literature, it would again be helpful to again peruse the following page "A Flawed Tool" below.
|
A Flawed Tool |
|
due to the false teaching and/or misunderstanding of the fundamentals |
|
|
|
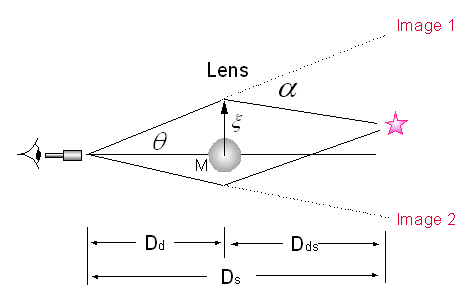
Ray Geometry Technique for Gravitational Lensing |
|
Researchers utilizing this tool seek alternative simplifications for the application of the cumbersome light bending rule of General Relative and may or may not be thoroughly familiar with the basic principle of the light bending rule of General Relativity given by Equation (1),
where
by the mainstream researchers dealing with this subject can only be either an innocent oversight or a deliberate deception. Equation (1) can be derived using the minimum-energy or least-time conservations of energy considerations (for details and Reference see: http://www.extinctionshift.com/details09.htm) and not simply by the use of simple, clumsy schemes of geometry such as the Ray Geometry Technique for Gravitational Lensing. The correct geometrical picture as well as the correct Mathematical Physics of the conservation of energy, the Physics of the minimum energy path or the minimum time path and the principle of reciprocity must all be considered for any correct interpretation of the observed astrophysical events dealing with gravitational lensing. From the above Figure depicting the so-called "Ray Geometry Technique for estimating Gravitational Lensing", the derived angle of Equation (3)
for estimating the gravitational deflection can not be an exact equivalence to that of General Relativity, i.e., that of Equation (1). It is readily see that, as the source approaches the vicinity of the gravitational lens, the adjustable parameter Dds , the distance between the source and the lens, gets smaller or approaches zero. Ds = 26,000 light years, where Ds is the distance between the observer and the source. Any lensing effect estimated by this geometrical "ray" scheme can only be a very poor approximation to that of General Relativity, where the derived angle given by Equation (3) will approach a very small value, i.e., zero as Dds approaches zero. This suggests incorrectly that the lensing effect would be minimized for sources located in proximity to or near to the gravitating mass or to the lens. Researchers not familiar with the Physics of gravitational lensing and the profound fundamentals thereof should not rely on such tools as the so-called "Ray Geometry Technique" used for the purpose of estimating Gravitational Lensing without taking the painstaking effort to apply the Profound Fundamentals of the phenomenon under observation. |
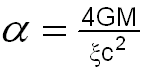 (1)
(1)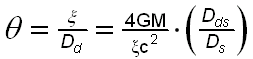 (3)
(3)