Significant Findings
Gauss's Law of Gravitation Correctly Applied
The CLEAR OBSERVATION EVIDENCE
-
If the light bending rule of General Relativity were actually valid, then the night sky should be filled with Einstein rings, since there are many instances where the observer, a star acting as a lens and another star that is acting as a source happen to lie on or close to a direct line-of-sight.
-
Within current technical means, the light bending effect of the sun should be easily detectable well beyond the thin plasma rim of the sun, in the plasma-free vacuum space for distances of several solar radii.
-
It is important to note that only microwaves resonate with the solar plasma and the dense electrons of solar winds. The solar winds have virtually no effects at all on the path or the propagation velocity of electromagnetic waves in the infrared, optical or ultraviolet portion of the spectrum.
-
The electron density profile of the solar winds have a measurable a frequency dependent and impact parameter dependent transit time effect on electromagnetic waves only in the microwave frequency spectrum (plasma resonace). (Shapiro Effect)
-
The light emitted from the rapidly moving stars, moving along precise elliptical paths about Sagittarius A*, strictly according to Kepler's laws, shows absolutely no evidence of a gravitational light bending effect or distortions as revealed in the recorded images of this region to this date; a region intensely observed by the astrophysicists since 1992.
Important Fundamentals of Mathematical Physics applied to Gravitational lensing
We shall apply the fundamental principle of the analytical Gaussian Surface Law, applicable directly to gravitation as well as to electromagnetism and the fundamental principle of optical reciprocity directly to the observational evidence.
These fundamental principles clearly show that a co-linear alignment of the observer, the lens and the source is totally unnecessary for an observation of a light bending effect, as predicted by the light bending rule of General Relativity.
Gauss's Surface Law applied to an Enclosed Gravitating Mass

Fig 1A Gauss's Spherical Surface law illustrated for Constant Mass Enclosed
Figure 1A illustrates a hypothetical constant but shrinking mass enclosed inside of an analytical Gaussian sphere. Gauss' Law states that the flux of the gravitational field through the Gaussian surface for a given constant mass enclosed, regardless of the size or radius of the enclosed mass sphere, is constant.
Gauss's Surface Law applied to an Enclosed Gravitating Mass (continued)
The gravitational effect on a ray of light at an impact parameter R would theoretically depend solely on the amount of Mass M that is enclosed within the analytical Gaussian sphere of radius R as illustrated in Fig 1B.
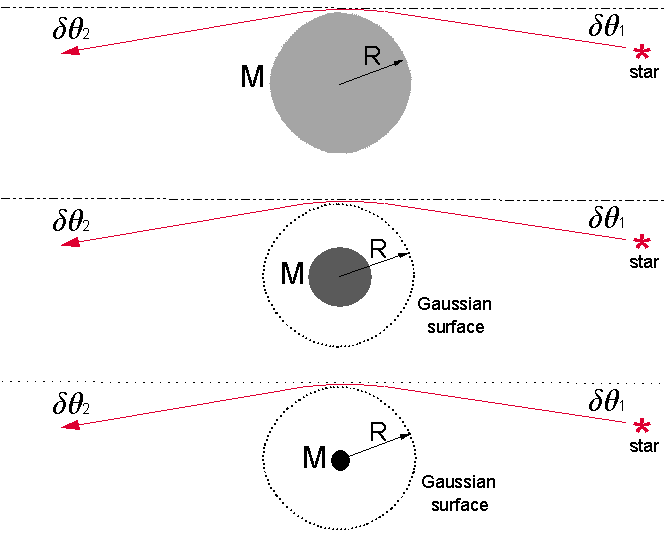
Fig 1B Gauss's Surface Law applied to Equal Gravitating Masses Enclosed
The gravitational effect that would be noted at the surface of an analytical Gaussian sphere does not care at all about the size or radius of the mass that is enclosed within the Gaussian sphere. We can see from Gauss's Law that the enclosed mass spheres of different radii and equal masses will present equal gravitational effects at the surface of the analytical Gaussian surface of radius R.