Significant Findings
Principle of Reciprocity demonstrated on Einstein Ring
as function of the distance to the light source
The images collected since 1992 from the orbiting stars about Sagittarius A* located at the galactic center have revealed absolutely NO distortions due to gravitational lensing effects as predict by General Relativity; NO evidence for gravitational light bending as illustrated in the recorded undistorted time resolved images of stellar objects orbiting about Sagittarius A*.
At the core of the Milky Way a major experiment in astrophysics is now brewing at this very moment. The past 10 years of astrophysical observations on the galactic core of the Milky Way reveal that the observed Kepler motion of the rapidly moving stars orbiting about Sagittarius A* appears to counter the predictions of General Relativity. The effect is understandable from a straight forward principle of Mathematical Physics that encloses the apparent galactic core mass inside of an analytical Gaussian spherical surface and from a principle of optical reciprocity on the path of a light ray that is predicted to bend under influence of the gravitating core mass as predicted by General Relativity. The principle of optical reciprocity simply states that the photons of light from any ray that joins the observer and the source would take exactly the same path in either direction. From the principle of equal gravitational effects for equal masses enclosed in an analytical Gaussian surface, it is clearly seen that a co-linear alignment of the observer, the lens and the source is totally unnecessary for any observation of a light bending effect predicted by General Relativity. A co-linear alignment is only a special case required for the Geometry of a perfectly constructed Einstein ring.
Any light ray that is gravitationally bent by a point-like gravitating mass, as is predicted by General Relativity, will always have an axis of symmetry which would be perpendicular to the line joining the source and the observer only when the lens is positioned exactly at the midpoint on the line joining the observer and the source. This is depicted in the animated illustration in Fig 6.
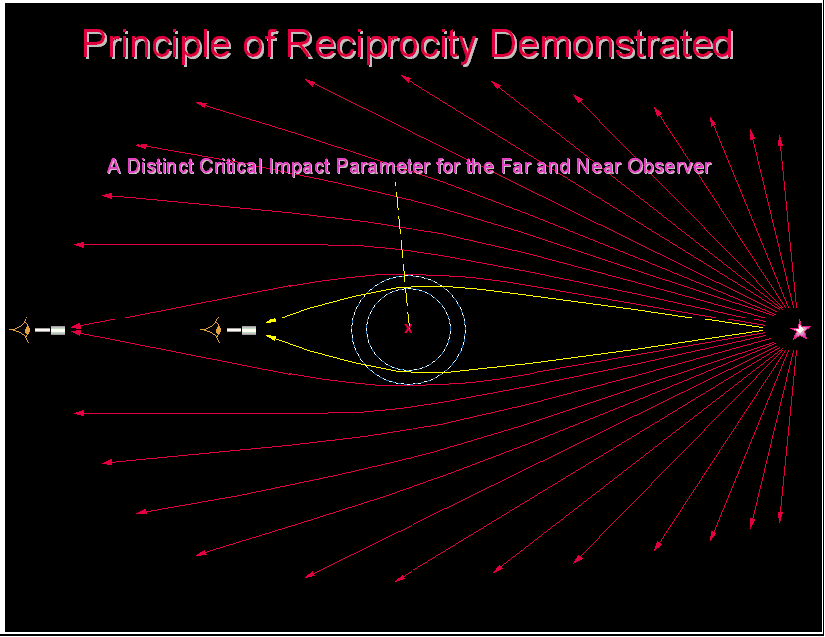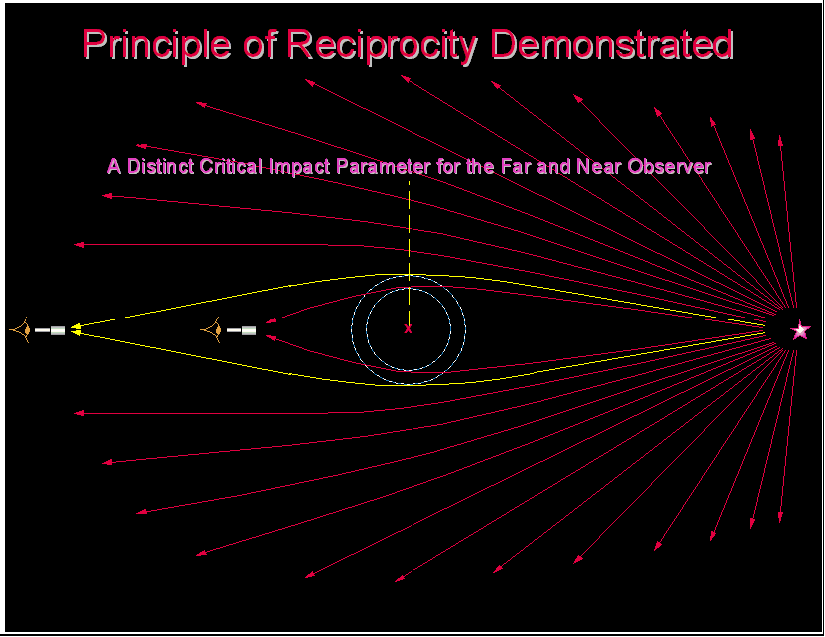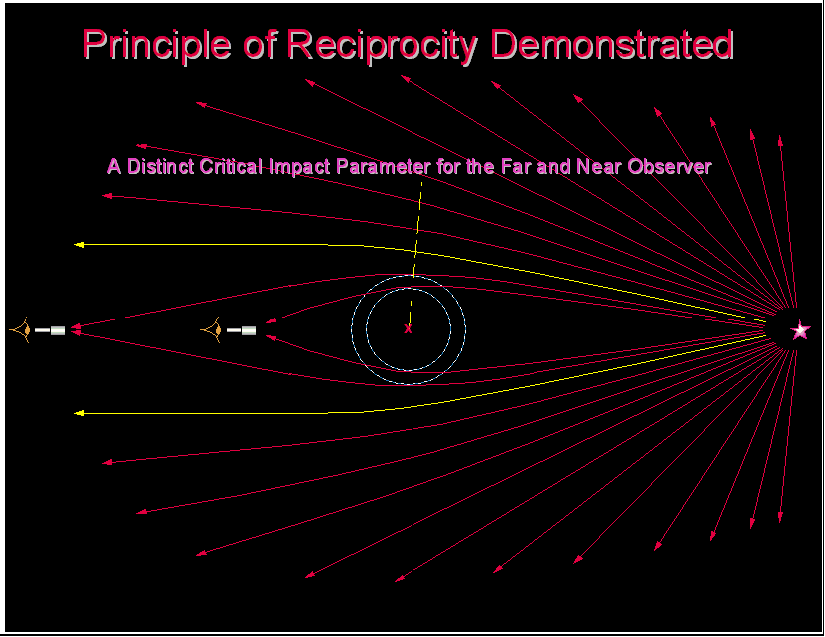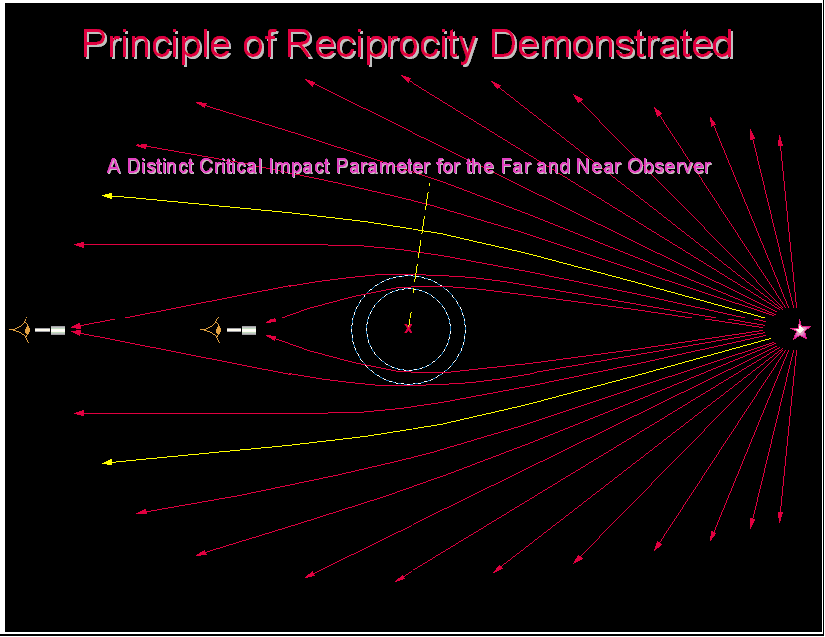
Fig 6 Ray Dependency of Near- and Far-field Observers
It is readily seen that the far-field observer and the near-field observer will collect the light of a completely different set of rays, depending on the geometry of the ray lensing, each ray with a correspondingly distinct axis of symmetry. The problem is actually a 3-dimensional problem which assumes the light collected by the observer is a set of rays wrapped around the line joining the source and the observer. The observers depicted here, both the near-field observer and the far-field observer, should see a theoretical Einstein ring as predicted by General Relativity. The axis of symmetry is perpendicular to the line joining the source and the observer only when the lens is exactly at the midpoint on the line joining the source and the observer; the special simplified case, most often explained in the elementary Physics textbooks.

Fig 6B What if the Source distance DSL is increased to infinity?
From the special case, assuming the validity of the light bending rule of General Relativity, as DSL approaches infinity, the observer would note that the radius of the Einstein ring in units of radians would increase to a maximum value give by
 DSL
= infinity.
DSL
= infinity.
IMPORTANT NOTE:
1) Light rays that do not cross can never produce an Einstein ring at the observer.
2) All co-linearly positioned observers, near and far, should theoretically have a corresponding set of crossing light rays at his point of observation; an observable Einstein ring.
3) We have seen from the fundamental principle of Gauss's Law that an exact co-linear alignment of the observer, the lens and the source is not required for an observation of lensing. Thus, all observers depicted above, whether near or far, should theoretically be able to detect some lensing effects, if not a perfect ring, of course, assuming again the validity of General Relativity.
Some popular lensing tools frequently used by modern astrophysicists and gravitational lensing experts, as depicted in the figure below, apparently did not use the principle of optical reciprocity and consider the lensing effects in the vicinity of the lens in their design considerations.
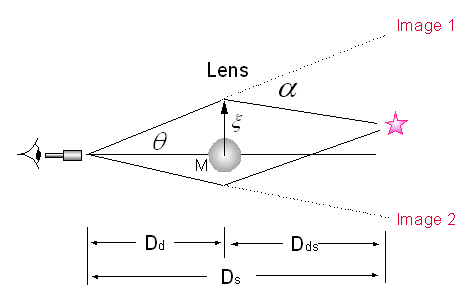
Fig 7 Ray Geometry Technique for Gravitational Lensing
Researchers utilizing this tool seek an alternative simplification for the application of the cumbersome light bending rule of General Relative and may or may not be thoroughly familiar with the basic principle of light bending of General Relativity given by the equation
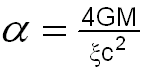 (1)
(1)
derived using General Relativity considerations! The geometry as well as the Physics of conservation of energy, the Physics of the minimum energy path, minimum time and the principle of reciprocity must all be considered for any correct interpretation of the astrophysical events.
From the above Figure, "Ray Geometry Technique for Gravitational Lensing", the angle
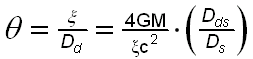 (2)
(2)
is derived. It is readily see that, as the source approaches the vicinity of the gravitational lens, where the adjustable parameter Dds is the distance between the source and the lens and Ds = 26,000 light years, the distance between the observer and the source, the lensing estimated by this equation (2), a modification of (1), approaches a very small value (approaches zero). This suggests incorrectly that the lensing effect described by (2) is minimized for sources in proximity to the gravitating mass, the lens.
It is important to note and recall that the principle of light bending of General Relativity given by Equation (1) and the Ray Geometry Technique for Gravitational Lensing given by Equation (2) are not the same equations, the main subject of the published paper.
The stellar sky presents vast opportunities to modern Astronomy and Astrophysics to allow for the detection of lensing events due to the large numbers of stellar objects that just happen to be positioned in a near perfect line-of-site to the earth based observers; again of course, assuming the validity of the light bending rule of General Relativity. With this in mind the entire celestial sky should be full of Einstein-rings.